Detailed Functional Description
The Algebraic Expression Library is a C++ library which evaluates expressions input in a standard C++ std::string. The expressions are standard C/C++ expressions and also includes C math library function like sin() and cos(). For a complete list look at the file algebraicfun.h. The library supports variable names of standard C/C++ and will allocate them or a C++ map<std::string,double> may be provide externally. Values are stored as double variables and the expression evaluator can decode hexadecimal in the form 0xnn, octal in the form 0nnn and binary in the form 0bnn... It also recognizes characters (char) in the form 'x' as well as control character in the form '\t' and '\xnn'.
The Interface Methods
First in order to use the library you must include the header file algebraicexpr.h or if you wish to include C math library functions algebraicfun.h.
#include "algebraicexpr.h"
or
#include "algebraicfun.h"
Note that algebraicfun.h will include algebraicexpr.h.
Constructors
This constructor is used to create an AlgebraicExpr object that when used in the null form will not allow variable allocation and will allocate an internal variable list. It can optionally allow variable allocation when it is invoked with argument "true". When variable allocation is false all variable must be allocated with the method AddVar(). Note that if you intend to use math functions simply substitute the class AlgebraicFun for AlgebraicExpr. The AlgebraicExpr is a base class of AlgebraicFun and it simply calls the base class constructors. The math functions are added through protected virtual methods so the interface is the same for both classes.
Parameters
- allow The optional variable allocation flag.
The null constructor.
AlgebraicExpr(bool allow = false);
This constructor is used to create an AlgebraicExpr object that is given a variable list and will not allocate an internal variable list. It can optionally allow variable allocation when it is invoked with a second argument "true". When variable allocation is false variable must be allocated with the method addVar() or added to the provided list.
- var The external variable list.
- allow The optional variable allocation flag.
The constructor with the external variable list.
AlgebraicExpr(map<string,double>& var,
bool allow = true);
Error Handling
All syntax error throw a ExprError. It's a public member of the AlgebraicExpr class.The Public methods.
Change the debug flag.
void debug(int d) { debug_flag = d; };
int debug() { return(debug_flag); };
Prints to stdout the text name of the token, used for debugging only.
void printTok(int token);
Variable Methods
If you choose to let AlgebraicExpr allocate variables these methods are how you access them. They will also work if you supply the variable list however you would have direct access. Note that the methods are virtual so they can be overridden by derived classes.
Retrieve the value of a given variable.
- n The variable name.
- Returns the value of the named variable.
virtual double getVar(string n);
Add a variable to the variable list. If no value is given
set it to zero.
- n The variable name.
- val The initial value.
- If variable does exist return true if it does not false.
virtual bool addVar(string n,
double val = 0.0 );
Set the value of a variable to the given value.
- n The variable name.
- val The new value.
- If variable does exist return true if it does not false.
virtual bool setVar(string n,double val);
The interface to the variable allocation flag.
- allow The allow allocation flag.
void variableAllocation(
bool allow = true);
The interface to the variable allocation flag turning it on or off with the ability to set the variable list.
- var The variable list.
- allow The allow allocation flag.
void variableAllocation(
map<string,double>& var,
bool allow = true);
Solving the Expression
This is the core method that takes an algebraic expression and returns the result as well as records the values of variable that were set. There are two variations of this method one which simply takes an expression and returns the resulting value. And one that is also given a variable list.- ex The expression.
- Returns the resulting value.
double solve(string ex);
- ex The expression.
- var The variable list.
- Returns the resulting value.
double solve(string ex,
map<string,double>& var
);
The Algorithms
There are three primary parts the Solve() method.
- Tokenisation of the Expression (The Lexer).
- Infix to Postfix Conversion.
- The Postfix Evaluator.
Tokenisation of the Expression
The tokenisation is accomplish by the lexer (lexical analyzer or tokenizer). In this case the lexer was produced by RE/Flex. The prime function of the lexer is identify and locate expression elements, commonly referred to as a token. The lexer processor returns the enumerator of the current token with it's text in a std::string and it length in a integer, are both passed by reference. The infix to postfix conversion code calls the lexer for each token. Processes the token and calls for the next token.
Infix to Postfix and The Postfix Evaluator
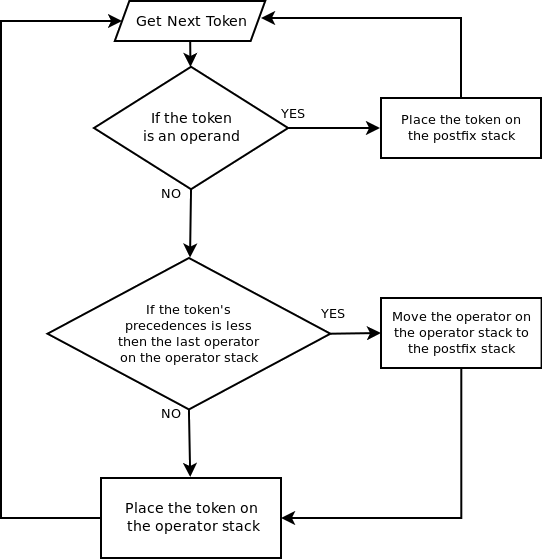
Infix or algebraic notation is of the form operand operator operand ( X + Y ). And postfix or reverse Polish notation is of the form operand operand operator ( X Y + ). Converting from infix to postfix is a common way of dealing with the problem of the order of evaluation. We are able to do the conversion and sort out the order of evaluation in one process. In this case our solution uses two stacks (they are actually vectors). One for temporary storage of operator. One which will be the postfix ordered operands and operators that will be handed to the postfix evaluator. Then the postfix evaluator will use another temporary stack where it places operands while it evaluate them.The expression is read from left to right. The lexer identify each expression element which we will refer to as a token one at a time. When the token is identified an ExprElement object is created and initialize with the token's information. The ExprElement is a protected class of the AlgebraicExpr class. It is the ExprElement object which is placed on the stacks. The general rule is if the token is an operand place it on the postfix stack. If the token is an operator and it precedence is higher or equal to the last operator placed on the operator stack, or if the operator stack is empty, then place the token on the operator stack. If the token's precedence is less move the last operator on the operator stack to the postfix stack and place the current token on the operator stack.
When the last token is processed the the token on the operator stack are moved on to the postfix stack piror to the evaluation process.
Infix to Postfix Conversion
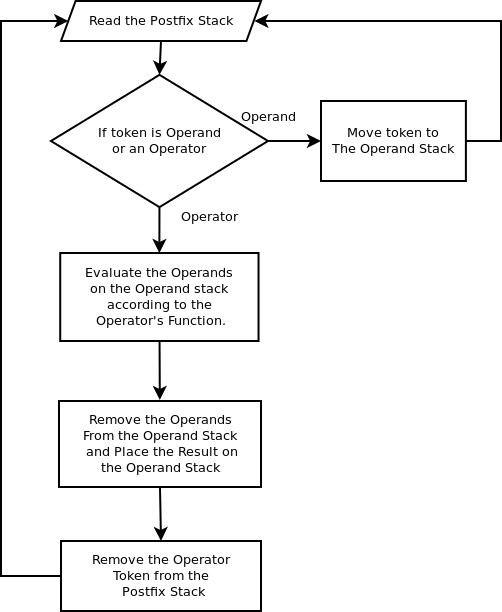
Postfix Evaluation
Order of Pecedences
| Name | Symbol | Associativity |
|---|---|---|
| Unary Operators | ++,--,!,~ | Right to Left |
| Multiplication and Division | *,/,% | Left to Right |
| Add and Subtract | +,- | Left to Right |
| Bitwise Shift | <<,>> | Left to Right |
| Bitwise AND | & | Left to Right |
| Bitwise Exclusive OR | ^ | Left to Right |
| Bitwise inclusive OR | | | Left to Right |
| Logical AND | && | Left to Right |
| Logical OR | || | Left to Right |
| Ternary Conditional | ?: | Right to Left |
| Assingments | =,+=,-=,*=,/=,%=, &=,^=,|=,<<=,>>= | Right to Left |
| Comma | , | Left to Right |
Let's look at how the conversion works.
Take the expression:
X = 4 + 3
The first token is the variable X which is an operand. So it's placed on the postfix stack. The next token is the equal sign =. So it's placed on the operator stack. Next the integer 4 that's placed on the postfix stack. Note that when we place an item on the stack it goes the button this is because the standard template vector uses a push_back() and a pop_back(). However this is not a problem because when we evaluate the postfix stack we will evaluate from top to bottom.
| operators | Postfix |
|---|---|
| = | X |
| 4 |
Then the plus sign +. It precedence is higher then the equal sign so we simply places it on the operator stack.
| operators | Postfix |
|---|---|
| = | X |
| + | 4 |
Then the integer 3.

| operators | Postfix |
|---|---|
| = | X |
| + | 4 |
| 3 |
Now let's move the operator to the postfix stack. Note the order.
| operators | Postfix | |
|---|---|---|
| X | << Start Here | |
| 4 | ||
| 3 | ||
| + | ||
| = |
Now the postfix evaluator starts at the top of the postfix stack where the X is. If the token is an operand it simply places it on the temporary stack. When it encounters an operator it executes the operation on the operands on the temporary operand stack.

| operands | Postfix |
|---|---|
| X | 4 |
| 3 | |
| + | |
| = |
| operands | Postfix |
|---|---|
| X | 3 |
| 4 | + |
| = |
| operands | Postfix |
|---|---|
| X | + |
| 4 | = |
| 3 |
Now it add the two operands on the temporary operand stack, removes them and places the answer back on the operand stack. Then it removes the operator from the postfix stack.
| operands | Postfix |
|---|---|
| X | = |
| 7 |
And in the final move X is assigned to the value 7.
Let's try another one. This one will deal with precedence.
Take the expression:
X = 4 * 3 + 2
Multiply has higher precedence then add. So this should evaluate to 14. That is 4 time 3 is 12 plus 2 is 14.
The first token is the variable X which is an operand. So it's placed on the postfix stack as above. The next token is the equal sign =. So it's placed the operator stack. Next the integer 4 that's placed on the postfix stack.
| operators | Postfix |
|---|---|
| = | X |
| 4 |
Then the multiply sign *. Note that the equal sign or the assignment operator is of a lower precedences then the multiply operator. So it's placed on the operator stack.
| operators | Postfix |
|---|---|
| = | X |
| * | 4 |
Then the integer 3.
| operators | Postfix |
|---|---|
| = | X |
| * | 4 |
| 3 |
Then the plus +. However the plus sign is a lower precedence then the multiply so we move the multiply to the postfix stack and place the plus on the temporary operator stack. Effectively changing the order of evaluation.
| operators | Postfix |
|---|---|
| = | X |
| + | 4 |
| 3 | |
| * |
Then the integer 2.
| operators | Postfix |
|---|---|
| = | X |
| + | 4 |
| 3 | |
| * | |
| 2 |
Now let's move the operator to the postfix stack. Note the order again.

| operators | Postfix | |
|---|---|---|
| X | << Start Here | |
| 4 | ||
| 3 | ||
| * | ||
| 2 | ||
| + | ||
| = |
Now let's evaluate. We starting by moving the operands to the temporary stack stopping when we see an operator.
| operands | Postfix |
|---|---|
| X | * |
| 4 | 2 |
| 3 | + |
| = |
First multiply 3 times 4. Get 12 remove 3 and 4 and place 12 on the stack. And now that we have multiplied remove it from the postfix stack. The 2 being an operand moves to the temporary operand stack.
| operands | Postfix |
|---|---|
| X | + |
| 12 | = |
| 2 |
Then add 2 to 12. Get 14 remove 12 and place 14 on the operand stack. And assign X the value 14.
| operands | Postfix |
|---|---|
| X | = |
| 14 |
We combined a couple of steps there however you should be able to see how it works.
Let's try another one. This one will deal with parentheses.
Take the expression:
X = 4 * ( 3 + 2 )
Now this time we have altered the order of evaluation with parentheses. So now we add 3 and 2 get 5 and multiply it by 4 to get 20.
And again the first token is the variable X which is an operand. So it's placed on the postfix stack as above. The next token is the equal sign =. So it's placed the operator stack. Next the integer 4 that's placed on the postfix stack.
| operators | Postfix |
|---|---|
| = | X |
| 4 |
Then the multiply sign *. And again the equal sign or the assignment operator is of a lower precedences then the multiply operator.
| operators | Postfix |
|---|---|
| = | X |
| * | 4 |
Then the open parentheses (. It's an operator and precedence is not a factor so place it on the operator stack.
| operators | Postfix |
|---|---|
| = | X |
| * | 4 |
| ( |
Then the integer 3. It's an operand so place it on the postfix stack.
| operators | Postfix |
|---|---|
| = | X |
| * | 4 |
| ( | 3 |
Then the plus sign +. It's an operator with a higher precedences then open parentheses so place it on the operator stack.
| operators | Postfix |
|---|---|
| = | X |
| * | 4 |
| ( | 3 |
| + |
Then the integer 2. It's an operand so place it on the postfix stack.
| operators | Postfix |
|---|---|
| = | X |
| * | 4 |
| ( | 3 |
| + | 2 |
Then the closing parentheses ). Now move all the operator on the operator stack to the postfix stack until the opening parentheses and discard it.
| operators | Postfix |
|---|---|
| = | X |
| * | 4 |
| 3 | |
| 2 | |
| + |
Now let's move the operator to the postfix stack. Note the order again.

| operators | Postfix | |
|---|---|---|
| X | << Start Here | |
| 4 | ||
| 3 | ||
| 2 | ||
| + | ||
| * | ||
| = |
Now let's evaluate. We starting by moving the operands to the temporary stack stopping when we see an operator.
| operands | Postfix |
|---|---|
| X | + |
| 4 | * |
| 3 | = |
| 2 |
Now we add 2 plus 3 get 5 remove 2 and 3 and place 5 on the operands stack. And remove the plus operator from the postfix stack.
| operands | Postfix |
|---|---|
| X | * |
| 4 | = |
| 5 |
Now multiply 5 times 4 get 20 remove 5 and 4 and place 20 on the operands stack. And remove the multiply operator from the postfix stack. And finally x is assigned the value of 20.
| operands | Postfix |
|---|---|
| X | = |
| 20 |
One thing to notice is that most operators such as *,/,+,- operate on two operands. However there are exceptions. We have already seen how the parentheses work. Another group is increments and decrements, both pre and post work with one operands and it must be a variable. The other group is C math library function which involve commas and closing parentheses. And they may have from one to three operands and between commas complete expression including other math functions.
Let's try an expression with a math function.
Take the expression:
X = pow( 4, 3 + 2 )
Now this time we have the function pow(), to raze to the power of an exponent xy. With an argument that is the expression 3 + 2. So first 3 + 2 is 5 and then take 4 to the power of 5 and get 1024.
And again the first token is the variable X which is an operand. So it's placed on the postfix stack as above. The next token is the equal sign =. So it's placed the operator stack. Next the function pow() ch has a higher precedences then the equals sign so it's placed on the operator stack.
| operators | Postfix |
|---|---|
| = | X |
| pow |
Then the integer 4.
| operators | Postfix |
|---|---|
| = | X |
| pow | 4 |
Then a comma ,. In the case of a comma we verify that the number of arguments for the given function warrants this comma and increment the comma count so if we encounter another one we can verify the argument count. In this case the function pow() has two arguments so the comma is justified. We only need to record the number of arguments so we discard the comma and go to next token.
Then the integer 3.
| operators | Postfix |
|---|---|
| = | X |
| pow | 4 |
| 3 |
Then the plus sign +.
| operators | Postfix |
|---|---|
| = | X |
| pow | 4 |
| + | 3 |
Then the integer 2.

| operators | Postfix |
|---|---|
| = | X |
| pow | 4 |
| + | 3 |
| 2 |
Then the closing parentheses ). All we need to do at this point is check that we have all argument we need for the pow() function. Then move the operators to the postfix shack.
| operators | Postfix |
|---|---|
| X | |
| 4 | |
| 3 | |
| 2 | |
| + | |
| pow | |
| = |
So now let's evaluate.
Move the operands.

| operators | Postfix |
|---|---|
| X | + |
| 4 | pow |
| 3 | = |
| 2 |
Start by adding 3 and 2 to get 5. Remove 3 and 2 and place 5 on the temporary operand shack.
| operators | Postfix |
|---|---|
| X | pow |
| 4 | = |
| 5 |
Now raze 4 to 5th power and get 1024.
| operators | Postfix |
|---|---|
| X | = |
| 1024 |
And finally assign the value 1024 to the variable X.
For more information: info@acmesoftwareworks.com


 Main Page
Main Page